optimización de funciones ejercicios resueltos , ejemplos y problemas con solución paso a paso desde cero matemáticas 1 2 bachillerato , selectividad EVAU EBAU
Ejercicios de optimización de funciones
Vamos a empezar con tres ejercicios clásicos de optimización de funciones
Ejercicio clásico 01 optimización de funciones ver solución
Encuentra dos números positivos cuya suma sea 120, tales que el producto de uno de ellos por el cuadrado del otro sea máximo.
Ejercicio clásico 02 optimización de funciones ver solución
De entre todos los rectángulos de perímetro 24 cm calcula el de área máxima
Ejercicio clásico 03 optimización de funciones ver solución
Un agricultor dispone de 3000 € para cercar un terreno rectangular, usando el río adyacente como lado con el fin de que el recinto sólo necesite 3 cercas. El coste de la cerca paralela al río es de 5 € por metro instalado, y el de la cerca para cada uno de los lados restantes es de 3 € por metro instalado. Calcula las dimensiones del terreno de área máxima que puede cercar con el presupuesto que tiene.
Subamos el nivel
Problemas de optimización de exámenes
Ejercicio clásico 04 optimización de funciones Ver solución
Se desea construir un depósito de chapa (en forma de prisma recto, abierto y de base cuadrada) con una capacidad de 32.000 litros ¿Cuáles han de ser las dimensiones del depósito para que se precise la menor cantidad de chapa posible en su construcción?
Ejercicio clásico 05 optimización de funciones Ver solución
Tenemos un cartón cuadrado de 6 cm de lado y queremos construir con él una caja sin tapa. Para ello recortamos un cuadrado de x cm de lado en cada vértice del cartón. Calcular x para que el volumen de la caja sea máximo.
Ejercicio clásico de examen Optimización EBAU SElectividad
De todos los rectángulos cuyo perímetro es de 40 cm , encontrar el que tiene la diagonal de menor tamaño
Ejercicio de examen SElectividad
Halla dos números mayores o iguales que 0, cuya suma sea 1, y el producto de uno de ellos por la raíz cuadrada del otro sea máximo
Ejercicio clásico de examen Optimización EBAU SElectividad 2023 NIvel FULL
Determinar los vértices del rectángulo de área máxima que tiene lados paralelos a los ejes de coordenadas y vértices en el borde del recinto delimitado por las gráficas de las funciones f(x)= x2 g(x) = 2 – x2
Ejercicio resuelto selectividad 2023
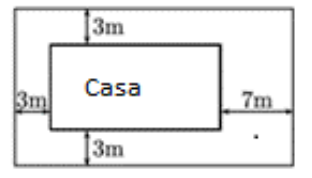
Se quiere construir una Casa de la Juventud de 240 m2 de superficie, que estará rodeada por una zona ajardinada con las dimensiones de la imagen. Si se quiere minimizar la superficie total de la zona ajardinada, ¿qué dimensiones debe tener la Casa de la Juventud? ¿Cuál es el área de la zona ajardinada?
Ejercicio clásico de examen Optimización EBAU Selectividad resuelto también con inteligencia artificial Te sorprenderá el resultado
Un ayuntamiento ha dividido en parcelas parte del terreno municipal no urbanizable y lo ha cedido a los vecinos para su cultivo. Uno de los vecinos ha decidido que en su parcela asignada utilizara como huerto una zona rectangular de 72 metros cuadrados, dejando el resto para plantar frutales e instalar una caseta donde guardar las herramientas necesarias. La zona de huerto estará dividida en dos partes: la parte dedicada al cultivo de hortalizas será un rectángulo interior separado de los lados que delimitan el huerto. La separación será de medio metro entre cada uno de los lados de mayor longitud y un metro entre cada uno de los lados de menor longitud. La franja que delimita la zona de hortalizas la dedicara al cultivo de flores y plantas aromáticas. a) (2 puntos) Calcule las dimensiones del huerto para que el área de la zona para el cultivo de hortalizas sea máxima. b) (0.5 puntos) Calcule el área de la zona de cultivo de hortalizas.
Para ser unas auténticas máquinas de optimización de funciones hay que plantear y resolver muchos ejercicios , ahí va una tanda de problemas que han caído en exámenes
Más problemas clásicos de optimización
de base cuadrada y tales que el perímetro de una cara lateral es de 30 cm,
halla las dimensiones del que tiene volumen máximo
Calcula las dimensiones del terreno de área máxima que puede cercar con el presupuesto que tiene.
Ejercicio resuelto Selectividad
CyL Junio 2013









8 comentarios
Porfa Sergio necesito tu ayuda esque tengo una duda del primer ejercicio de optimización. Cuando dice el producto de uno de ellos por el cubo del otro yo había puesto (x3·y) y tu lo has puesto al contrario, entonces al sustituir (y) la (x) me ha dado 18, o sea lo que a ti te ha dado la (y). Como sabes si lo tienes que hacer poniendole el cubo a la (Y) o a la (x) ??
Lo tienes bien cualquiera de los dos métodos esta bien
Vale muchas gracias;)
Tengo un problemilla, a ver si podrías ayudarme a resolverlo.
Dispuesto a obtener la máxima capacidad de almacenaje, te planteas cuáles serán las dimensiones óptimas de ancho, largo y alto para ello. Un amigo que trabaja en el aeropuerto te comenta además que las que tienen la base rectangular con el lado del rectángulo doble que el ancho, son las que mejor caben en los compartimentos del avión, con lo que se haces un esquema con la situación:
El esquema es tal que el ancho = x / alto = 2x (El largo se desconoce)
A su vez, la suma del alto + largo + ancho no debe superar los 115 cm
¿Sabrás resolverlo para que el volumen de almacenaje sea óptimo? ¿Y qué volumen sera éste?
Debes buscar la relación y la función: te lo dejo en una imagen mi planteamiento y solución:
http://postimg.org/image/encgxzb3j/
Hola necesito ayuda con este problema. Descomponer el numero 9 en dos sumas tal wue la suma x^2+6y se minima. Muchas gracias
Las páginas de un libro deben medir cada una 600 cm2 de área. Sus márgenes laterales y el inferior miden 2 cm. y el superior mide 3 cm. Calcular las dimensiones de la página que permitan obtener la mayor área impresa posible.—— me pueden ayudar con este problema
el 15 es muy parecido