Ejercicios resueltos de exámenes de probabilidad , diagramas de árbol , teorema de BAYES , probabilidad condicionada ,probabilidad total . Selectividad PAU y pruebas de acceso 1 , 2 bachillerato y universidad
Recopilación de ejercicios resueltos de probabilidad de diferentes exámenes
Ejercicio resuelto modelo selectividad 2024
La selección española competirá en la Copa Mundial Femenina de Futbol 2023. En los dos primeros partidos de la fase de grupos, que consta de tres partidos, la probabilidad de ganar cada uno de ellos es del 80%. Sin embargo, debido al aumento en la moral de las jugadoras, si ganan los dos primeros partidos la probabilidad de ganar el tercero asciende al 90 %. En caso contrario, la probabilidad de ganar el tercer partido se mantendrá en el 80 %. Se pide: a) (0.5 puntos) Determinar la probabilidad de que la selección española no gane ningún partido durante la fase de grupos. b) (1 punto) Calcular la probabilidad de que la selección gane el tercer partido de la fase de grupos. c) (1 punto) Si sabemos que la selección ha ganado el tercer partido, determinar la probabilidad de que no haya ganado alguno de los dos encuentros anteriores
Problema resuelto de selectividad CLÁSICO DE EXAMEN EVAU 2022
De una cesta con 6 sombreros blancos y 3 negros se elige uno al azar. Si el sombrero es blanco, se toma, al azar, un pañuelo de un cajón que contiene 2 blancos, 2 negros y 5 con cuadros blancos y negros. Si el sombrero es negro, se elige, al azar, un pañuelo de otro cajón que contiene 2 pañuelos blancos, 4 negros y 4 con cuadros blancos y negros. Se pide:
a) (1 punto) Calcular la probabilidad de que en el pañuelo aparezca algún color que no sea el del sombrero.
b) (0.5 puntos) Calcular la probabilidad de que en al menos uno de los complementos (sombrero o pañuelo) aparezca el color negro.
c) (1 punto) Calcular la probabilidad de que el sombrero haya sido negro, sabiendo que el pañuelo ha sido de cuadros.
madrid matemáticas aplicadas a las ciencias sociales
En una bolsa hay cuatro bolas rojas y una verde. Se extraen de forma consecutiva y sin reemplazamiento dos bolas. Calcúlese la probabilidad de que:
a) Las dos bolas sean del mismo color.
b) La primera bola haya sido verde si la segunda bola extraída es roja.
madrid matemáticas aplicadas a las ciencias sociales
Ver solución
Selectividad matemáticas sociales Castilla y León Junio 
Probabilidad Libro vídeo
Selectividad matemáticas sociales Castilla y León Junio
3B Una fábrica de piezas para aviones está organizada en tres secciones. La sección A fabrica el 30% de las piezas, la sección B el 35%, mientras que el resto se fabrican en la sección C. La probabilidad de encontrar una pieza defectuosa es del 0.01, 0.015 y 0.009 según se considere la sección A, B o C, respectivamente. a) Calcula la probabilidad de que una pieza elegida al azar salga defectuosa de dicha fábrica. b) Si elegida una pieza al azar es defectuosa, ¿qué probabilidad hay de que sea de la sección B?
Selectividad matemáticas sociales Castilla y León Junio 2014 .
4B– Se elige al azar un número de 4 cifras distintas escrito con las cifras 7, 2, 3 y 8. Calcula la probabilidad de que dicho número sea mayor que 7500
Selectividad matemáticas sociales Castilla y León Junio 2013
3A– Según el informe anual La Sociedad de la Información 2012, el 63% de los usuarios de móvil en España tiene un “Smartphone”. Entre los propietarios de este tipo de teléfono, el 77% lo emplea para su conexión habitual a internet. Sin embargo, entre los propietarios de otros tipos de teléfono móvil sólo el 8 % lo emplea para la conexión habitual a internet.
- a) Calcula la probabilidad de conectarse habitualmente a internet a través del teléfono móvil.
- b) Si un usuario emplea habitualmente el teléfono móvil para conectarse a internet, halla la probabilidad de que sea propietario de un “Smartphone”.
Selectividad matemáticas sociales Castilla y León Junio 2013
4A En una ciudad, la probabilidad de que llueva un día de junio es del 10%, y de que haga sol un 75 %. Si no es posible que en un mismo día de junio llueva y haga sol simultáneamente, ¿cuál es la probabilidad de que en un día de junio no llueva ni haga sol? Ver solución
Selectividad matemáticas sociales Castilla y León Junio 2013
4B– El 60% de los clientes de una frutería compran naranjas y el 30% no compra ni naranjas ni manzanas. ¿Qué porcentaje de clientes compra manzanas, pero no naranjas? Ver solución
Selectividad matemáticas sociales Castilla y León Junio 2012
Un moderno edificio tiene dos ascensores para uso de los vecinos. El primero de los ascensores es usado el 45% de las ocasiones, mientras que el segundo es usado el resto de las ocasiones. El uso continuado de los ascensores provoca un 5% de fallos en el primero de los ascensores y un 8% en el segundo. Un día suena la alarma de uno de los ascensores porque ha fallado. Calcula la probabilidad de que haya sido el primero de los ascensores.
Selectividad matemáticas sociales Castilla y León Junio 2012
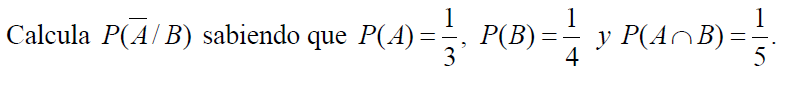
selectividad matemáticas sociales Madrid Junio 2011 3 A
Ejercicio 3
En un edificio inteligente dotado de sistemas de energía solar y eólica, se sabe que la energía suministrada cada día proviene de placas solares con probabilidad 0.4, de molinos eólicos con probabilidad 0.26 y de ambos tipos de instalaciones con probabilidad 0,12. Elegido un día al azar, calcúlese la probabilidad de que la energía sea suministrada al edificio:
a) por alguna de las dos instalaciones,
b) solamente por una de las dos. ver solución
Selectividad matemáticas sociales Castilla y León Septiembre 2009
3A– Hay una epidemia de gripe. Un síntoma muy común es el dolor de cabeza, pero este síntoma también se presenta en personas que tienen un catarro común y en personas que no tienen ningún trastorno serio. La probabilidad de tener dolor de cabeza, padeciendo gripe, catarro y no teniendo nada serio es 0.99, 0.5 y 0.004 respectivamente. Por otra parte, se sabe que el 10% de la población tiene gripe, el 15% catarro y el resto nada serio. Se desea saber:
a) Elegida al azar una persona, ¿qué probabilidad hay de que tenga dolor de cabeza?
b) Se sabe que una determinada persona tiene dolor de cabeza, ¿cuál es la probabilidad de que tenga gripe?
Ebau Castilla y león Mates aplicadas a las ciencias sociales
La lista electoral de un determinado partido político está formada por un número igual de hombres y mujeres. Un análisis sociológico de dichas listas revela que el 60% de los hombres tienen 40 o más años de edad, mientras que el 30% de las mujeres tienen menos de 40 años. Se elige al azar una persona que forma parte de las listas electorales.
- a) Calcula la probabilidad de que tenga menos de 40 años.
- b) Sabiendo que tiene 40 o más años de edad, calcula la probabilidad de que sea mujer.
