Aprenderemos a resolver ecuaciones de segundo grado , también llamadas cuadráticas , desde cero , paso a paso , tanto las completas que resolveremos por la fórmula , como las ecuaciones incompletas , aprenderemos varios trucos , incidiremos en las claves y trabajaremos los clásicos errores que se cometen para sacar NOTAZA en los exámenes , para ello realizaremos varios ejercicios clásicos de exámenes y aprenderemos a plantear y resolver todo tipo de problemas , cuando acabes con este tutorial , me dirás oye Sergio ponme ejercicios más difíciles que ya soy una máquina .
Así que … Vamos máquina !!!! ver TUTORIAL EN VÍDEO PARA SER UNA MÁQUINA
Qué son las ecuaciones de segundo grado
Una ecuación de segundo grado es aquella en la que la incógnita está elevada como máximo al cuadrado , y tiene la forma:
ax2+bx+c=0
Tipos de ecuaciones de segundo grado.
Decimos que una ecuación es completa si todos sus términos son distintos de cero :
ax2+bx+c=0
Decimos que una ecuación es incompleta si alguno de sus términos es cero b=0 ó c=0 , fíjate que a no puede ser cero porque entonces no habría x2 y entonces no sería una ecuación de segundo grado , twendrán alguna de estas formas:
ax2+bx+=0 ax2+c=0 ax2=0
¿Cómo se resuelve una ecuación de segundo grado completa?
ax2+bx+c=0
Este tipo de ecuaciones se resuelve aplicando la fórmula general :
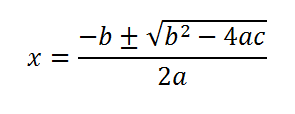
Para resolver estas ecuaciones tendremos que sustituir los valores de a,b y c en la fórmula , pero ten cuidado no cometas los clásicos errores , para ello te daré la chapa en los ejercicios resueltos en vídeo
Número de soluciones de una ecuación de segundo grado
Estas ecuaciones pueden tener dos soluciones , una solución o ninguna solución , esto en matemáticas es muy importante así que vamos a aprenderlo genial.
Llamamos discriminante a la parte que está dentro de la raíz en la fórmula general Δ=b2-4ac
Si el discriminantes es positivo , tenemos dos soluciones
Si el discriminante es cero, tenemos una solución
Y si el discriminante es negativo no tenemos solución .
Ejemplos y ejercicios resueltos de ecuaciones de segundo grado completas
Hemos visto la teoría pero para realmente convertirnos en auténticas máquinas lo mejor es que practiquemos con los siguientes ejercicios resueltos en vídeo ver solución
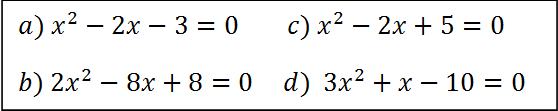
Ecuaciones de segundo grado Incompletas
Incompletas tipo ax2+bx=0
Esgte tipo la resolvemos sacando factor común x , en el video siguiente aprenderás a resolverlas y te enseñaré un truco
Ejemplos
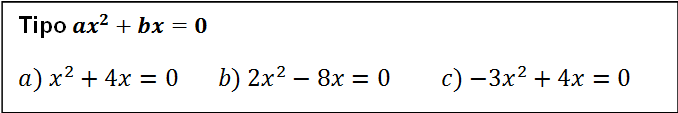
Incompletas tipo ax2+c=0
Resolvemos como una ecuación de primer grado y luego hacemos la raíz CUIDADO al hacer la raíz que tenemos que poner la solución positiva y la negativa
Ejemplo
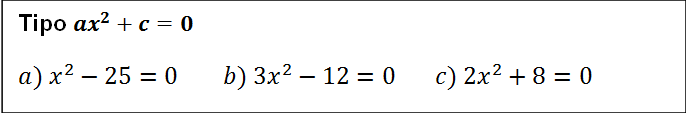
Problemas de ecuaciones de segundo grado
Ahora que ya somos unas máquinas resolveindo las ecuaciones de segundo grado , vamos a resolver problemas de ecuaciones de segundo grado , incidiendo en el planteamiento que es la parte que más » problemas » nos dará.
Si tienes algún problema interesante , déjamelo en los comentarios de los videos y si me gusta realizaremos un vídeo .
Problema 01
La suma de los cuadrados de dos números naturales consecutivos es 41 Halla dichos números. Ver solución
Problema 02
La suma de los cuadrados de dos números pares naturales consecutivos es 100 Halla dichos números. Ver solución
Rectángulos
Problemas de ecuaciones de 2º grado 03
El área de un rectángulo es de 40 cm2. Si la base es 3 cm mayor que la altura ¿Cuál es el perímetro del rectángulo? Ver solución
Problemas de ecuaciones de 2º grado 04
Los lados de un rectángulo se diferencian en 4 cm y su área mide 96 cm2 ¿Cuál es el perímetro del rectángulo? Ver solución
Triángulos
Problemas de ecuaciones de 2º grado 05
El cateto mayor de un triángulo rectángulo mide 2 cm menos que la hipotenusa y 2 cm más que el cateto menor. Calcula la medida de los tres lados ver solución
Problemas de ecuaciones de 2º grado 06
Calcula las longitudes de los lados de un triángulo rectángulo si son tres números naturales consecutivos ver solución
OTRAS ENTRADAS QUE TE PUEDEN INTERESAR
Problemas de ecuaciones NUMERICOS
Taller de Matemáticas TVE ( la aventura del Saber) Capítulo 01
sustitución sistemas de ecuaciones lineales