Ejercicios de divisibilidad , criterios de divisibilidad , descomposición de un número en factores primos , como calcular el mínimo común múltiplo mcm , máximo común divisor MCD y problemas 2 ESO 1 ESO
DIVISIBILIDAD ejercicios resueltos
ÍNDICE
Criterios de divisibilidad Ejercicios resueltos
Descomposición factorial de un número en factores primos
Cómo Calcular el mínimo común múltiplo y el máximo común divisor Ejercicios
Problemas de máximo común divisor y mínimo común múltiplo MCD y mcm
Definiciones Divisibilidad
Múltiplo de un número Los múltiplos de un número son los diferentes resultados de multiplicar un número por los números naturales ( sin contar el 0). Por ejemplo los múltiplos de 12 son : 12,24,36,48,60,72,….
Divisibilidad Decimos que un número es divisible entre otro si al hacer la división el resto es cero ( es decir que la división es exacta)
Criterios de divisibilidad
Divisibilidad entre 2 Un número es divisible entre 2, si es un número par
Divisibilidad entre 3 Un número es divisible entre 3, si la suma de sus cifras es un múltiplo de 3.
Divisibilidad entre 5 Un número es divisible entre 5, si termina en 0 o en 5
Ejercicio resuelto

Números primos y compuestos
Decimos que un número es primo si solo tiene dos divisores , el 1 y si mismo . Si un número no es primo se dice que es compuesto .
IMPORTANTE: Principales números primos
2,3,5,7,11,13,19,23,29
Descomposición de un número en factores primos.
La factorización de un número consiste en expresarlo como producto de números primos elevados a los exponentes correspondientes. Esta factorización es única.
Para descomponer un número en factores primos , lo dividimos entre 2 tantas veces sea posible, después entre 3,entre 5 … y así sucesivamente entre números primos hasta obtener el 1
Ejercicio resuelto
Halla la descomposición en factores primos de :
a) 36 b)60 c)126 d)72 e)90
Mínimo común múltiplo y máximo común divisor
Antes de comenzar debes dominar la descomposición en factores de un número , sino la dominas mira este ejercicio resuelto
Ejercicio resuelto
Halla la descomposición en factores primos de :
a) 36 b)60 c)126 d)72 e)90
Múltiplos y divisores comunes a varios números. Máximo común divisor y mínimo común múltiplo de dos o más números naturales.
El máximo común divisor MCD , de varios números es el mayor de sus divisores
El mínimo común múltiplo m.c.m , de varios números es el menor de sus múltiplos comunes
Pasos para calcular el mínimo común múltiplo , m.c.m
Paso 1 Descomponemos los números en factores primos ( Factorización de un número)
Paso 2 Se eligen los factores NO comunes y comunes elevados al MAYOR exponente
Paso 3 Se multiplica lo octenido en el paso 2
Pasos para calcular el Máximo Común Divisor de varios números MCD
Paso 1 Descomponemos los números en factores primos ( Factorización de un número)
Paso 2 Se eligen los factores comunes elevados al menor exponente
Paso 3 Se multiplica lo octenido en el paso 2
Los procedimientos de los cálculos del M.C.D y del m.c.m son muy parecidos vamos a compararlos para que no hayan dudas
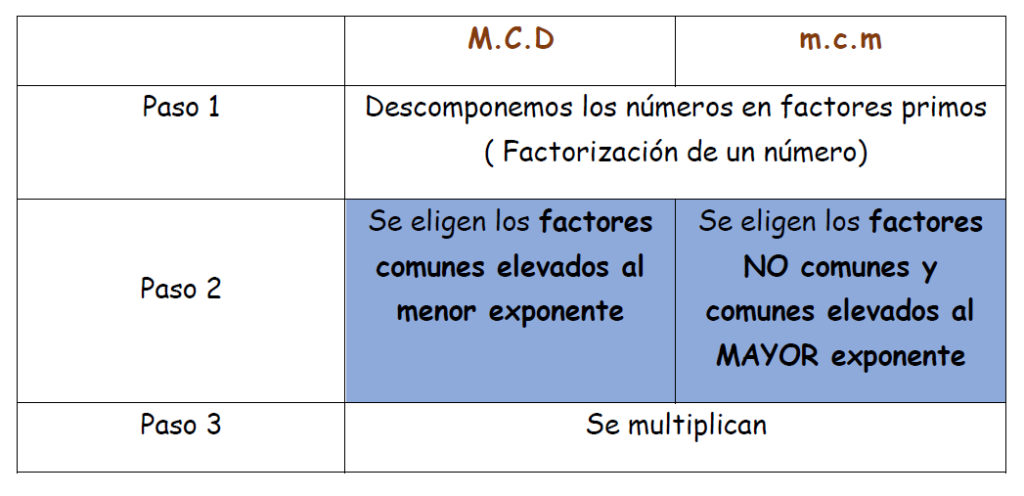
Ejercicios resueltos cálculo del mínimo común múltiplo y máximo común divisor
Ejercicio resuelto 01 Calcula
a) m.c.m (28,10) c) m.c.m (72,90)
b) M.C.D (28,10) d) M.C.D (72,90)
Problemas de máximo común divisor y mínimo común múltiplo MCD y mcm
Ejercicio 01 resuelto
Tenemos dos listones de madera de longitudes 72 y 60 centímetros Si tenemos que cortarlos en trozos iguales de forma que obtengamos el mayor número de trozos ¿cuántos trozos debemos cortar y cuanto deben medir? Ver solución
Ejercicio 02 resuelto
En una expedición llegan víveres en helicóptero cada 8 días y en barco cada 12 días , Si hoy 3 de Junio han coincidido ambos medios de transporte , ¿ Qué día volverán a coincidir ? Ver solución
Ejercicio 03 resuelto
Se desean envasar 48 botes de espárragos y 54 botes de pimientos del Bierzo, en cajas con el mismo número de botes y sin mezclar los productos en la misma caja ¿cuál es el número mínimo de cajas necesarias? ¿Cuántos botes irán en cada caja? Ver solución
OTRAS ENTRADAS QUE TE PUEDEN INTERESAR
Problemas sistemas de dos ecuaciones con dos incógnitas
CURSO DE FÍSICA Y QUÍMICA 2 ESO








