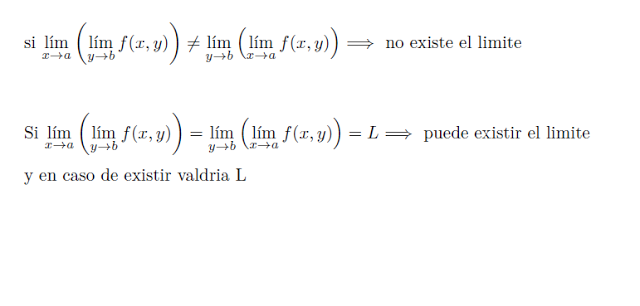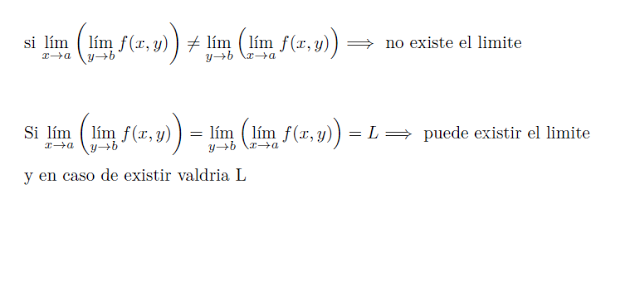2.1
Cálculo y existencia de límite de una función de varias variables
Cálculo y existencia de límite de una función de varias variables
MUY IMPORTANTE si
existe el límite de una función de varias variables este es único
existe el límite de una función de varias variables este es único
Calcular los siguientes
límites
límites
a) $displaystylelim_{(x,y)
to{(-1,3)}}{frac{2x-y}{x^2+y^2}}$
to{(-1,3)}}{frac{2x-y}{x^2+y^2}}$
b) $displaystylelim_{(x,y)
to{(1,1)}}{frac{x+y}{2x+y}}$
to{(1,1)}}{frac{x+y}{2x+y}}$
c) $displaystylelim_{(x,y)
to{(0,0)}}{(x+y)senleft(frac{pi }{x+y}right)}$
to{(0,0)}}{(x+y)senleft(frac{pi }{x+y}right)}$
d) $displaystylelim_{(x,y)
to{(0,1)}}{(x^2)cosleft(frac{2x+y }{x}right)}$
to{(0,1)}}{(x^2)cosleft(frac{2x+y }{x}right)}$
2.2
caso (0/0) en el que podemos factorizar
caso (0/0) en el que podemos factorizar
a)$displaystylelim_{(x,y)
to{(0,0)}}{frac{x^2-y^2}{x+y}}$
to{(0,0)}}{frac{x^2-y^2}{x+y}}$
b)$displaystylelim_{(x,y) to{(0,0)}}{frac{4x^2-y^2}{2x-y}}$
c)$displaystylelim_{(x,y)
to{(0,0)}}{frac{3x+2y}{9x^2-4y^2}}$
to{(0,0)}}{frac{3x+2y}{9x^2-4y^2}}$
d)$displaystylelim_{(x,y)
to{(0,0)}}{frac{x+y}{x^2+2xy+y^2}}$
to{(0,0)}}{frac{x+y}{x^2+2xy+y^2}}$
2.3
caso (0/0) Para este caso debemos realizar una serie de
pasos para demostrar la No existencia del límite o la existencia del límite y
su valor. Nos vamos a basar en la propiedad de que si existe el límite este debe de ser único .
caso (0/0) Para este caso debemos realizar una serie de
pasos para demostrar la No existencia del límite o la existencia del límite y
su valor. Nos vamos a basar en la propiedad de que si existe el límite este debe de ser único .
2.3.1 limites reiterados o sucesivos en
funciones de varias variables
funciones de varias variables
si $displaystylelim_{x to{a}}{left(displaystylelim_{y to{b}{}}{f(x,y)}right)neqdisplaystylelim_{y to{b}}{left(displaystylelim_{x to{a}{}}{f(x,y)}right)$ $Longrightarrow{}$ no existe el limite
Si $displaystylelim_{x to{a}}{left(displaystylelim_{y to{b}{}}{f(x,y)}right)=displaystylelim_{y to{b}}{left(displaystylelim_{x to{a}{}}{f(x,y)}right)=L$ $Longrightarrow{}$ puede existir el limite y en caso de existir valdria L
Ejemplo1 Calcular
los límites reiterados o sucesivos de los siguientes límites y decir si No
existe el límite o si puede existir el límite
los límites reiterados o sucesivos de los siguientes límites y decir si No
existe el límite o si puede existir el límite
a)$displaystylelim_{(x,y)
to{(0,0)}}{frac{xy}{x^2+y^2}}$
to{(0,0)}}{frac{xy}{x^2+y^2}}$
b)$displaystylelim_{(x,y)
to{(0,0)}}{frac{x^2-y^2}{x^2+y^2}}$
to{(0,0)}}{frac{x^2-y^2}{x^2+y^2}}$
2.3.2 limites radiales o direccionales
en funciones de varias variables Si la solución de algún
límite radial o direccional depende de m , entonces no existirá el límite
en funciones de varias variables Si la solución de algún
límite radial o direccional depende de m , entonces no existirá el límite
Ejemplo 1
Calcula los siguientes
límites radiales o direccionales mediante el cambio y= mx de las siguientes
funciones de varias variables en el origen y decir si No existe el límite o si
puede existir el límite .
límites radiales o direccionales mediante el cambio y= mx de las siguientes
funciones de varias variables en el origen y decir si No existe el límite o si
puede existir el límite .
a)$f(x,y)=frac{3x^2y}{x^2+y^2}$
b)$f(x,y)=frac{2xy}{2x^2+y^2}$
Ejemplo 2
Calcula los siguientes
límites radiales o direccionales mediante el cambio y= mx e y=mx2 de las siguientes funciones
de varias variables en el origen y decir si No existe el límite o si puede
existir el límite .
límites radiales o direccionales mediante el cambio y= mx e y=mx2 de las siguientes funciones
de varias variables en el origen y decir si No existe el límite o si puede
existir el límite .
a)$f(x,y)=frac{2y^2-x^4}{x^4+y^2}$
Ejemplo 3
Calcula los siguientes
límites radiales o direccionales mediante el cambio e x=my2 de las siguientes funciones
de varias variables en el origen y decir si No existe el límite o si puede
existir el límite .
límites radiales o direccionales mediante el cambio e x=my2 de las siguientes funciones
de varias variables en el origen y decir si No existe el límite o si puede
existir el límite .
a)$f(x,y)=frac{2y^2x}{y^4+2x^2}$
Ejemplo 4
Demostrar que no existe el
siguiente límite
siguiente límite
a)$displaystylelim_{(x,y) to{(0,0)}}{frac{3xy}{x^2+2y^2}}$