campo gravitatorio física 1 bachillerato 2 bachillerato y universidad . Ejercicios resueltos paso a paso desde cero hasta ser unas máquinas . Ley de gravitación universal , energía potencial , trabajo , potencial gravitatorio , planetas , velocidad orbital , velocidad de escape , fuerza , vectores , escalares , gravedad
CAMPO GRAVITATORIO
Ley de gravitación universal Fuerza gravitatoria
Todos los cuerpos del universo se atraen con una fuerza directamente proporcional a sus masas e inversamente proporcional al cuadrado de la distancia que las separa
Ver explicación fórmulaver explicación vectores
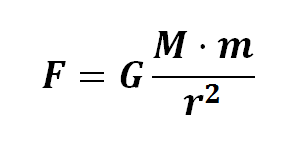
Siendo :
F la fuerza en Newton de atracción (N)
M y m masas en Kg
r la distancia que las separa en metros
G la constante de gravitación universal ( G= 6,67·10-11 N·m2/Kg2 )
Ejercicio 1 ley de gravitación universal
En el punto A(2,0) se sitúa una masa de 2 kg y en el punto B(-3,0) se coloca otra masa de 4 kg. Calcula la fuerza resultante que actúa sobre una tercera masa de 1 kg cuando se coloca en el origen de coordenadas ver solución
Ejercicio 2 ley de gravitación universal
En el punto P(3,0) se sitúa una masa de 5 kg y en el punto Q(0,2) se coloca otra masa de 4 kg. Calcula la fuerza resultante que actúa sobre una tercera masa de 2 kg cuando se coloca en el origen de coordenadas ver solución
Ejercicio 3 ley de gravitación universal
En el punto A(3,0) se sitúa una masa de 15 kg y en el punto B(0,0) se coloca otra masa de 10 kg. Calcula la fuerza resultante que actúa sobre una tercera masa de 2 kg cuando se coloca en el punto C(3,4). ver solución
recuerda que si esta página te ha servido , ayúdanos a crecer compartiéndonos por las redes sociales y por los grupos de whastsapp y SUSCRIBETE a youtube : http://goo.gl/CMFnu0 activando la campanilla , ya que en época de exámenes subimos muchos ejercicios clásicos de examen y nunca se sabe
Intensidad Campo gravitatorio
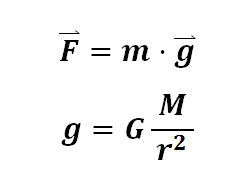
Siendo
g la intensidad de campo gravitatorio ( gravedad ) en N/kg ó m/s2
F la fuerza en Newton (N)
M y m masas en Kg
r la distancia que las separa en metros (m)
G la constante de gravitación universal ( G= 6,67·10-11 N·m2/Kg2 )
Ejercicio 01 Intensidad de campo gravitatorio
En el punto A(2,0) se sitúa una masa de 2 kg y en el punto B(-3,0) se coloca otra masa de 4 kg. Calcula la intensidad de campo gravitatorio en el origen de coordenadas ver solución
Ejercicio 02 Intensidad de campo gravitatorio
En el punto P(3,0) se sitúa una masa de 5 kg y en el punto Q(0,2) se coloca otra masa de 4 kg. Calcula el vector intensidad de campo gravitatorio en el origen de coordenadas .
b) Calcula el vector fuerza resultante que actúa sobre una masa de 2 kg cuando se coloca en el origen de coordenadas ver solución
Ejercicio 03 Intensidad de campo gravitatorio
En el punto A(0,0) se sitúa una masa de 15 kg y en el punto B(3,0) se coloca otra masa de 10 kg. Calcula la intensidad de campo gravitatorio en el punto C(0,4). ver solución
Ejercicio clásico de examen Punto donde se anula el Campo / fuerza
Recientemente la NASA envió la nave ORION-Artemis a las proximidades de la Luna. Sabiendo que la masa de la Tierra es 81 veces la de la Luna y la distancia entre sus centros es 3,84·105 km. Calcule en qué punto, entre la Tierra y la Luna, la fuerza ejercida por ambos cuerpos sobre la nave es cero
PRINCIPIO DE SUPERPOSICIÓN Campo gravitatorio (Masas Puntuales)
Clásico de examen
Dos masas puntuales de 100Kg están situadas en A(0,0) y B(6,0) medidas en metros
a) Calcula el campo gravitatorio y el potencial en los puntos C(3,0) y en D( 3,4)
b) Si dejamos en reposo una masa de 5Kg en el punto D , calcula su velocidad al llegar al punto C

Siendo
g la intensidad de campo gravitatorio ( gravedad ) en N/kg ó m/s2
F la fuerza en Newton (N)
M y m masas en Kg
r la distancia que las separa en metros (m)
G la constante de gravitación universal ( G= 6,67·10-11 N·m2/Kg2 )
Ejercicio 01 Energía potencial gravitatoria
En el punto A(4,0) se sitúa una masa de 8 kg y en el punto B(0,2) se coloca otra masa de 10 kg.
a)Calcula el potencial de campo gravitatorio en el origen de coordenadas
b)Si sobre el origen se sitúa una masa de 3 Kg calcular su energía potencial ver solución
Ejercicio 02 Energía potencial gravitatoria
En el punto A(4,0) se sitúa una masa de 10 kg y en el punto B(0,-2) se coloca otra masa de 20 kg. Calcular la energía potencial que tendrá una masa de 5 Kg situada en el origen de coordenadas ver solución
Trabajo en el campo gravitatorio
W=-m·(Vf V0)
Si W>0 el trabajo lo realiza el campo gravitatorio
Si W<0 el trabajo lo realiza una fuerza exterior al campo
Ejercicio 01 trabajo en el campo gravitatorio
Una partícula de masa de 2 kg está situada en el origen y otra partícula de masa de 4 kg está colocada en el punto A(6,0). Calcula el potencial gravitatorio en los puntos de coordenadas P(3,0) y Q(3,4). ¿Qué trabajo se realiza al transportar una masa de 5 kg desde el punto P hasta el punto Q?ver solución
Ley de gravitación universal Planetas Campo gravitatorio
Velocidad orbital o de órbita
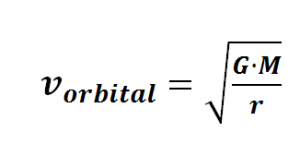
Ejercicio velocidad orbital
Calcular la velocidad orbital de un satélite de masa m=1500Kg que esta orbitando a una altura de 200 Km ver solución
Datos Rt=6370 Km Mt= 5,98·1024 Kg G=6,67·10-11 N·m2/kg2
Velocidad de escape
ver demostración de la fórmula
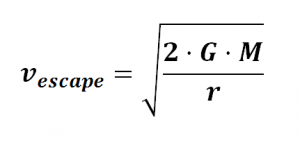
Ejercicio 01 velocidad de escape
Calcular la velocidad de escape de una nave de masa m=1500Kg lanzado desde la superficie terrestre ver solución
Datos Rt=6370 Km Mt= 5,98·1024 Kg G=6,67·10-11 N·m2/kg2
Periodo orbital
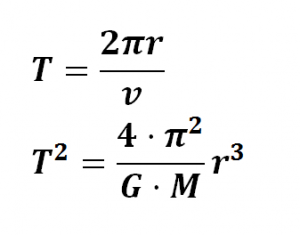
Ejercicio 01 Periodo orbital
Calcular la masa del sol sabiendo que la distancia de la tierra al sol es de 1,496·1011 m ver solución
Datos Rt=6370 Km Mt= 5,98·1024 Kg G=6,67·10-11 N·m2/kg2
Energía mecánica
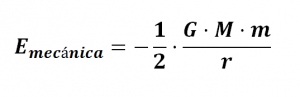
Ejercicio 01 Energía mecánica
Calcular la energía mecánica de un satélite de 1000 kg de masa en una órbita terrestre de radio 7000 Km ver solución
Datos Rt=6370 Km Mt= 5,98·1024 Kg G=6,67·10-11 N·m2/kg2
Energía o trabajo comunicada (trabajo necesario )
E necesaria +Ec0 +Ep0=Ecf+Epf
Ejercicio 01 Energía necesaria
Calcular la energía necesaria para poner un satélite de masa 1500 kg en una órbita terrestre de altura 200km ver solución
Datos Rt=6370 Km Mt= 5,98·1024 Kg G=6,67·10-11 N·m2/kg2
FORMULARIO
FORMULARIO CAMPO GRAVITATORIO
Energía de Satelización
CHEOPS es un satélite de la Agencia Espacial Europea, de 300 kg de masa, que se encuentra orbitando a 700 km de altura sobre la superficie terrestre en una órbita aproximadamente circular. Calcule la energía requerida para que, desde la superficie de la Tierra, el satélite pasara a describir dicha órbita.
Datos : G = 6,67·10–11 N·m2·kg–2 ;RT = 6,37·106 m ;MT = 5,98·1024 kg
recuerda que si esta página te ha servido , ayúdanos a crecer compartiéndonos por las redes sociales y por los grupos de whastsapp y SUSCRIBETE a youtube : http://goo.gl/CMFnu0 activando la campanilla , ya que en época de exámenes subimos muchos ejercicios clásicos de examen y nunca se sabe
EJERCICIOS DE EXÁMENES
01 Selectividad EBAU
Un satélite artificial de 500Kg de masa se lanza desde la superficie terrestre hasta situarlo en una órbita circular situada a una altura h=1200 Km sobre la superficie de la tierra . Determina:
a) la intensidad del campo gravitatorio terrestre en cualquier punto de la órbita descrita por el satélite
b) La velocidad del satélite cuando se encuentre en dicha órbita
Datos Rt=6370 Km Mt= 5,98·1024 Kg G=6,67·10-11 N·m2/kg2
02 Selectividad EBAU
Calcula el periodo de giro de la Luna en su movimiento circular alrededor de la Tierra
Datos: Masa de la Tierra= 5,97×1024 kg; Masa Luna= 7,35·1022 Kg ;
distancia tierra-Luna=3,84·108 m
03 Selectividad EBAU
Un satélite de 200 kg describe una órbita circular de 600 Km sobre la superficie terrestre:
a)Deduce la expresión de la velocidad orbital
- b) Calcular el periodo de giro
- c) Calcular la energía mecánica
Datos Rt=6370 Km G=6,67·10-11 N·m2/kg2
04 Selectividad EBAU
La masa de la Luna es 0,012 veces la masa de la Tierra, el radio lunar es 0,27 veces el radio de la Tierra y la distancia media entre sus centros es 60,3 radios terrestres.
a) Calcule la gravedad en la superficie lunar.
b) ¿En qué punto intermedio entre la Tierra y la Luna se equilibran las fuerzas que ambas ejercen sobre un cuerpo de masa m? Realice un esquema ilustrativo de las fuerzas.
05 Selectividad EBAU
Calcule: Ver parte 1 parte 2 parte 3
- a) La densidad media del planeta Mercurio, sabiendo que posee un radio de 2440 km y una
intensidad de campo gravitatorio en su superficie de 3,7 N/kg
- b) La energía necesaria para enviar una nave espacial de 5000 kg de masa desde la superficie del planeta a una órbita en la que el valor de la intensidad de campo gravitatorio sea la cuarta parte de su valor en la superficie.
Dato: Constante de la Gravitación Universal G=6,67·10-11 N·m2/kg2
06 Selectividad EBAU
El planeta A tiene tres veces más masa que el planeta B y cuatro veces su radio.
Obtenga:
- a) La relación entre las velocidades de escape desde las superficies de ambos planetas.
- b) La relación entre las aceleraciones gravitatorias en las superficies de ambos planetas
07 Selectividad EBAU
Un cohete de masa 2 kg se lanza verticalmente desde la superficie terrestre de tal manera que alcanza una altura máxima, con respecto a la superficie terrestre, de 500 km.
Despreciando el rozamiento con el aire, calcule:
- a) La velocidad del cuerpo en el momento del lanzamiento. Compárela con la velocidad de escape desde la superficie terrestre.
- b) La distancia a la que se encuentra el cohete, con respecto al centro de la Tierra, cuando su velocidad se ha reducido en un 10 % con respecto a su velocidad de lanzamiento.
Datos Rt=6370 Km Mt= 5,98·1024 Kg G=6,67·10-11 N·m2/kg2
08 Selectividad EBAU
Dos planetas, A y B, tienen el mismo radio. La aceleración gravitatoria en la
superficie del planeta A es tres veces superior a la aceleración gravitatoria en la superficie del planeta B. Calcule:
a) La relación entre las densidades de los dos planetas.
b) La velocidad de escape desde la superficie del planeta B si se sabe que la velocidad de escape desde la superficie del planeta A es de 2 km/s
OTRAS ENTRADAS QUE TE PUEDEN INTERESAR:
EXAMENES PROBABILIDAD DISTRIBUCION NORMAL Y BINOMIAL
Física 2º Bachiller ejercicios resueltos
PRINCIPIO DE SUPERPOSICIÓN (Masas Puntuales)









12 comentarios
Muchísimas gracias!!!!!!
muy bueno
Gracias!!!!
¿no hay mas ejercicios de este tipo? gracias con antemano
Por ahora sólo tengo los que hay en esta entrada
La semana q viene voy subir los de selectividad de Madrid y Castilla y leon
Por ahora sólo tengo los que hay en esta entrada
La semana q viene voy subir los de selectividad de Madrid y Castilla y leon
Por ahora sólo tengo los que hay en esta entrada
La semana q viene voy subir los de selectividad de Madrid y Castilla y leon
te amo Sergio
Quién no ama a Sergio?
Sergio, podrías añadir las explicaciones a cada uno de los apartados de física de segundo de bachillerato? Me vendría muy bien, gracias.
Sergio, podrías añadir las explicaciones a cada uno de los temas de la física de segundo de bachillerato? Me vendría muy bien, gracias.
Podrías realizar un tema sobre el campo electrostático? Gracias
Hola Sergio,
Quería saber si tenes ejercicios de electrostática resueltos. Ley de Coulomb y campo eléctrico. Muchas gracias