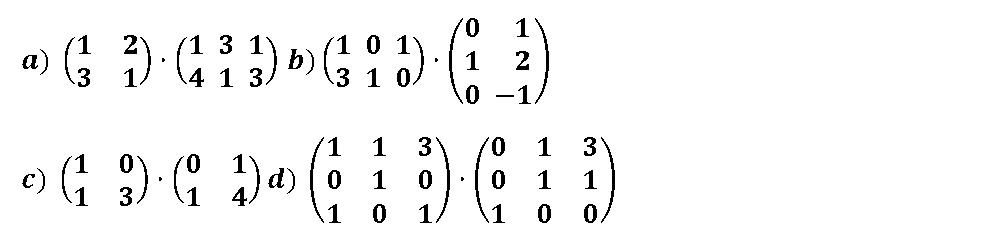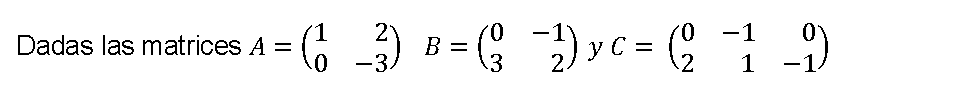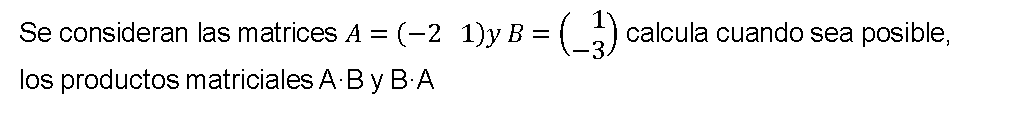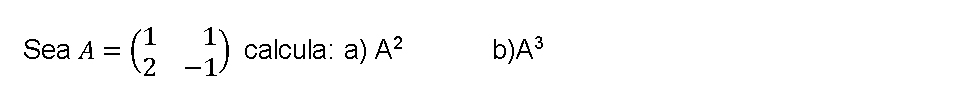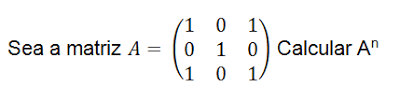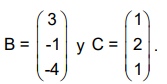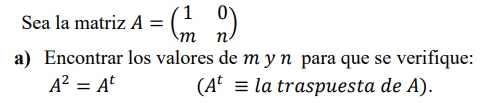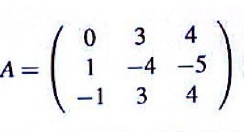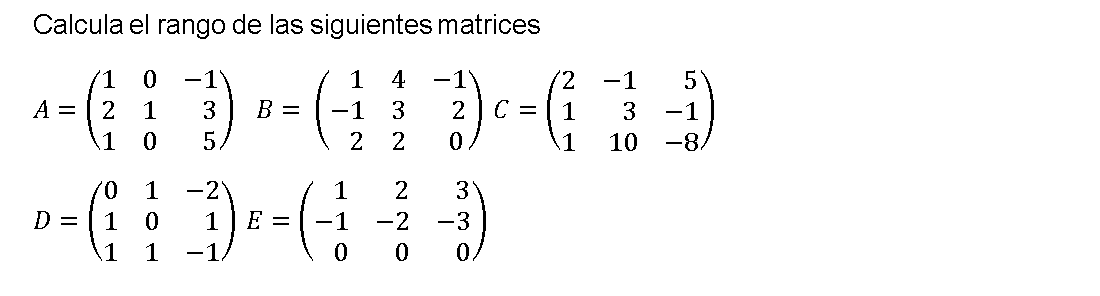Matrices ejercicios resueltos paso a paso matemáticas 2 bachillerato y universidad , aprenderemos desde cero , tipos de matrices , operaciones con matrices , producto , potencia , sistemas de ecuaciones , rango de una matriz
MATRICES
Nomenclatura de matrices y tipos
¿Qué es una matriz?
Es un conjunto de números ordenados en filas y columnas
Dimensiones de una matriz
Las dimensiones de una matriz se expresan como FilasxColumnas ( truco FerroCarril)
Ejemplo Ver vídeo
Elementos de una matriz
Son los números que componen la matriz, su notación es aij , siendo i el número de fila y j el número de columna
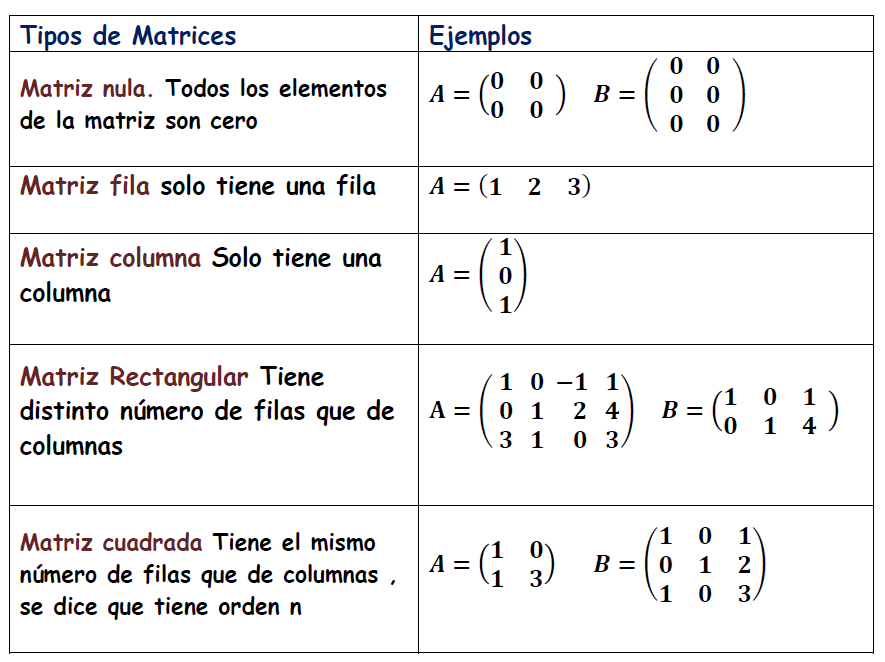
Tipos de matrices
Matriz nula. Todos los elementos de la matriz son cero
Matriz fila solo tiene una fila
Matriz columna Solo tiene una columna
Matriz Rectangular Tiene distinto número de filas que de columnas
Matriz cuadrada Tiene el mismo número de filas que de columnas , se dice que tiene orden n
Vamos a ver mejor los tipos de matrices en un cuadro resumen
Tipos de matrices cuadradas
Dentro de las matrices cuadradas hay los siguientes tipos :
Matriz Triangular Es una matriz cuadrada que tiene nulos todos los términos situados por debajo ( triangular superior ) o por encima ( triangular inferior ) de la diagonal principal
Matriz diagonal Es una matriz cuadrada en que todos los términos que NO están en la diagonal principal son cero
Matriz escalar Es una matriz diagonal en que todos los términos de la diagonal principal son iguales
Matriz identidad o unidad
Es una matriz diagonal en que todos los términos de la diagonal principal son unos
vamos a hacer un cuadro resumen
Matriz simétrica y antisimétrica
Matriz simétrica Es una matriz cuadrada donde los elementos simétricos respecto a la diagonal principal son iguales
Matriz Antisimétrica o hemisimétrica Es una matriz cuadrada donde los elementos de la diagonal principal son cero y los simétricos respecto a la diagonal principal son iguales pero de signo opuesto
vamos a verlo con un cuadro resumen
Matriz transpuesta At
Se obtiene cambiando las filas por columnas
Ejemplo ver solución
Operaciones con matrices
Suma y resta de matrices
Para sumar y restar matrices las matrices tienen que tener las mismas dimensiones, (es muy intuitivo)
Operaciones con matrices ejercicios resueltos
Opera ver solución
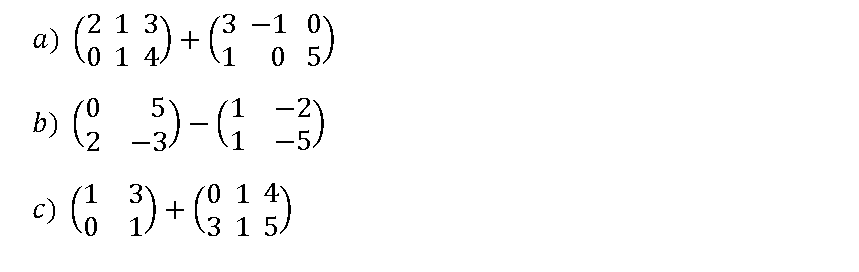
Producto de un número (escalar) por una matriz
Multiplicamos todos los elementos de la matriz por el número
Ejemplo
Opera ver solución
Sistemas de ecuaciones matriciales
Ejercicio resuelto ver solución
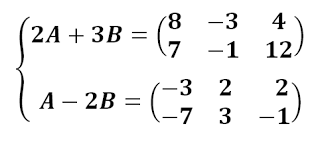Producto de matrices
Antes de aprender a multiplicar matrices vamos a ver dos propiedades Súper importantes del producto de matrices
Propiedad 1 El producto no es conmutativo
A·B ≠ B·A
Propiedad 2 Antes de multiplicar primero siempre tenemos que verificar que se pueden multiplicar, para que se puedan multiplicar , el número de columnas de la primera matriz tiene que ser igual al número de columnas de la segunda matriz
A3×2·B2×4=C3×4
A3×2·B3×2= No se pueden multiplicar
Otras propiedades
(A·B)·C=A·(B·C)
A·(B+C)= A·B +A·C
I·A=A·I=A
Vamos a aprender a multiplicar matrices con un ejemplo, no es complicado pero si algo lioso, tendremos que cogerle el “ ritmillo” para ello practicaremos
Ejercicios de matrices resueltos Producto
Ver solución apartados b ,c y d
Ejercicios resueltos operaciones con Matrices 01
Calcula cuando sea posible:
a) 2A+3B b) 3A-4C c) A·B
d) A·C e) C·A
Matrices que conmutan
Clásico de examen ver solución
Ejercicio resuelto de multiplicación de matrices EBAU
Ejercicios de matrices resueltos
ver solución aparatado a ver solución apartado b
Potencia de Matrices
Importante: Sólo existen potencias de matrices cuadradas
Potencia de una matriz 2×2 ejercicios resueltos
Potencia de una matriz 3×3 ejercicios resueltos
Matrices cíclicas
Ejercicio resuelto ver solución
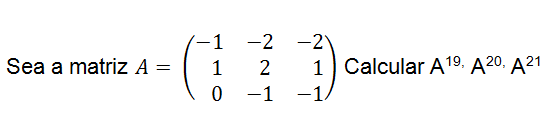
Potencia por recurrencia
Ejercicio resuelto ver solución
Ejercicio resuelto ver solución
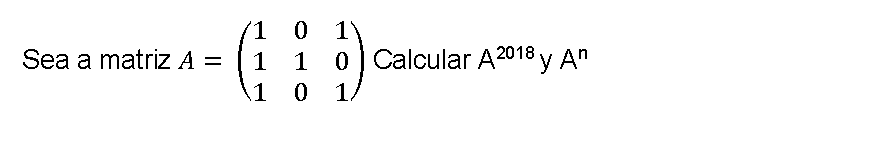
Ejercicio clásico de examen
Ejercicio resuelto ver solución
EJERCICIOS DE EXÁMENES DE MATRICES RESUELTOS
Si pronto tienes examen los siguientes ejercicios están sacados de los exámenes de selectividad EBAU EVAU de los últimos años , así que están genial para practicar de cara a los exámenes
EJERCICIO RESUELTO VER SOLUCIÓN
Ejercicio resuelto VER SOLUCIÓN
Sean
Calcular cuando sea posible las matrices C·Bt , Bt·C , B·C donde Bt es la matriz traspuesta de B
Ejercicios resuelto VER SOLUCIÓN
Ejercicios resueltos VER SOLUCIÓN
Sea
Calcular A2023 , A2024 , A2025
Ejercicio resuelto VER SOLUCIÓN
Ejercicio resuelto potencia
Rango de una matriz por el método de gauss
Definición El rango de una matriz es el número de filas o columnas linealmente independientes, pero lo mejor es ver cómo se calcula mediante unos ejemplos
Rango de una matriz por el método de gauss Ejercicios resueltos 01
Rango de una matriz por el método de Gauss Ejercicios resueltos 02
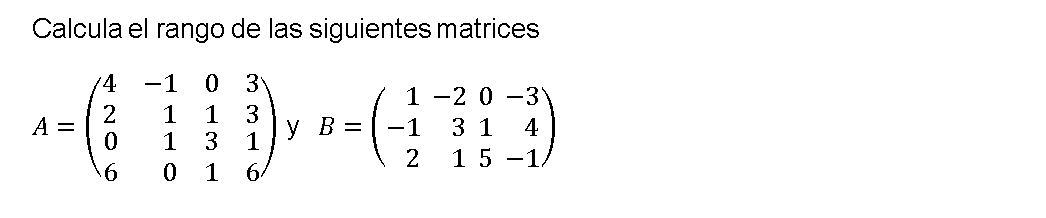
Rango de matrices 4×4 ejercicio resuelto
Matriz Inversa por el método Gauss-Jordan
Propiedades de la matriz inversa
Sea A una matriz cuadrada de orden n , entonces existe la matriz inversa de A <─>Ran(A)=n
Si existe A-1 decimos que A es una matriz regular o inversible
Si no existe A-1 decimos que A es una matriz singular
Propiedad Si A y B son matrices regulares del mismo orden entonces existe (A·B)-1 y (A·B)-1= B-1· A-1
Propiedad importante Si existe A-1 es única y A· A-1= A-1·A=I
Cálculo de una matriz inversa 2×2 por el método de Gauss-Jordan
Ejemplo 1 Matriz inversa 2×2 por el método Gauss-Jordan
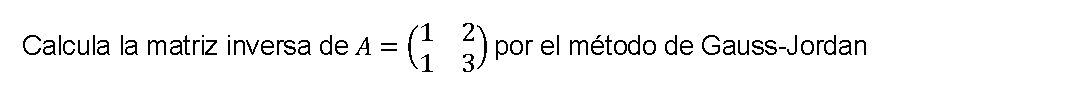
Ejemplo 2 Matriz inversa 2×2 por el método Gauss-Jordan
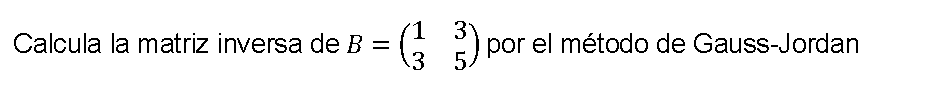
Calculo de una matriz 3×3 por el método de Gauss-Jordan
Ejemplo 1 Matriz inversa 3×3 por el método Gauss-Jordan
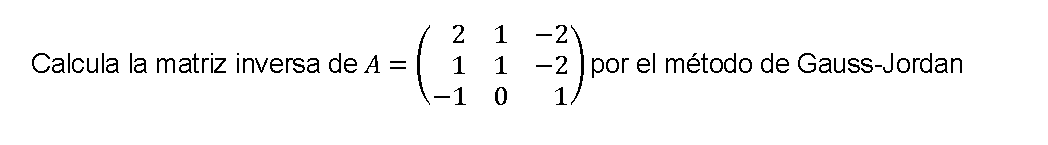
Ejemplo 2 Matriz inversa 3×3 por el método Gauss-Jordan
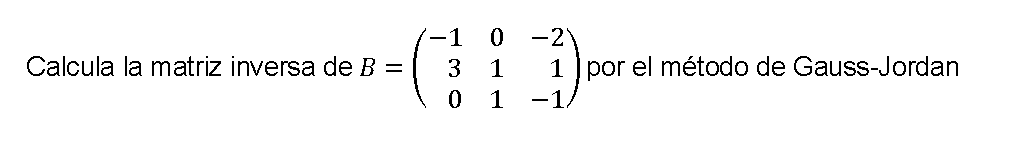
Inversa de una matriz con calculadora Ver vídeo
Otros TEMAS que os pueden interesar
Sistemas de Ecuaciones Método de Gauss
Integrales indefinidas , métodos de integración
CURSOS
Matemáticas 1º bachillerato ciencias sociales
Matemáticas 1º bachillerato ciencias y tecnológico
Matemáticas 2º bachillerato ciencias y tecnológico
Matemáticas 2º bachillerato ciencias aplicadas a las ciencias sociales
UNIVERDIDAD Matemáticas Física Química y Estadística
Discontinuidad evitable de salto finito e infinito
Método de Gauss Ejercicios Resueltos paso a paso
Equilibrio Químico grado de disociación 2 bachillerato
