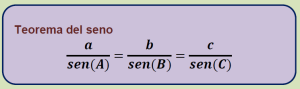Vamos a realizar varios ejercicios y problemas de resolución de triángulos , muy clásicos de exámenes de trigonometría.
Para no lesionarnos vamos a empezar calentando con un par de problemas
Problema
Las diagonales de un rombo miden 10 y 14 cm, respectivamente. Calcula el lado del rombo y sus ángulos. Ver solución
Problema
De un triángulo isósceles conocemos su lado desigual de 20 cm y su altura de 8 cm ¿ cuánto miden sus ángulos? Ver solución
Problema Cálculo de áreas trigonometría
Calcular la apotema y el área de un octógono regular cuyo lado mide 10 cm Ver solución
Problemas Aplicaciones a la topografía clásicos de examen
Problema
Desde un cierto lugar a nivel del suelo se ve la terraza de un edificio con un ángulo de elevación de 60º .Si nos alejamos 20m del edificio, el ángulo de elevación es de 30º . Hallar la altura del edificio. Ver solución
Problema
En la llanura desde un punto medimos el ángulo de elevación a una montaña y se obtiene 35º Acercándose a la montaña una distancia de 200 m se vuelve a medir el ángulo y se obtienen 55º. ¿ cual es la altura de la montaña? Ver solución
Problema
Se quiere medir la anchura de un río, para lo cual nos en una de las orillas y dirigimos la visual a un poste que se encuentra en la otra orilla obteniendo un ángulo de 53º. Al alejarnos de la orilla perpendicularmente un total de 20 m y mirar de nuevo el poste el ángulo es ahora de 32º. ¿Cuánto mide el río de ancho? Ver solución
Problema
Dos personas separadas 1200 m observan un OVNI que vuela entre ellos con ángulos de elevación de 35º y 55º ¿ a que altura vuela el OVNI? Ver solución
Problema
Una antena de radio esta sujeta al suelo mediante dos cables que forman con la antena ángulos de 36º y 48º. Si los puntos de sujeción de los cables al suelo y el pie de la antena se encuentran alineados y a una distancia total de 100 m, calcula la altura de la antena. Ver solución
Ahora vamos a hacer un problema sin calculadora
Sin usar la calculadora calcula la anchura de un río y la altura de un árbol que se encuentra en una de las orillas , sabiendo que desde la otra orilla se observa su parte más alta bajo un ángulo de 60º y si retrocedemos 5 m el ángulo es ahora de 30º Ver solución
Teorema del seno y coseno Problemas
IMPORTANTE
Hasta ahora solamente hemos resuelto triángulos rectángulos , por lo que los hemos resueltos por las razones trigonométricas , seno , coseno y tangente .
Los siguientes ejercicios serán todo tipo de triángulos y los resolveremos por el teorema del seno y del coseno
Cómo y cuándo usar el teorema del seno y del coseno
En el siguiente ejercicio que es un súper clásico de examen ,veremos cómo decidir que teorema usar
Ejercicios resueltos clásico de examen
Halla la distancia que hay entre dos barcos C y D, sabiendo que hemos medido la distancia que hay entre dos puntos de la costa A y B hemos obtenido 450 m y que con el teodolito hemos obtenido CAD= 48º , BAD= 57º ABC= 42º y CBD=53º
Vamos a hacer otro ejercicio que también es muy clásico de examen
E En un triángulo uno de los lados es el doble del otro y el ángulo opuesto a ese lado menor mide 30º Calcula cuanto mide cada uno de los otros ángulos ver solución
OTROS EJERCICIOS DE TRIGONOMETRÍA QUE TE PUEDEN INTERESAR
Convertir radianes a grados
RESOLUCIÓN DE TRIÁNGULOS RECTÁNGULOS
Problemas de Triángulos resueltos
TRUCO Razones trigonométricas de 0º 30º 45º 60º 90º
Circunferencia Goniométrica Explicación y TRUCOS
Fórmulas y TRUCOS Relaciones entre razones trigonométricas
RAZONES TRIGONOMÉTRICAS RELACIONES
EJERCICIOS RESUELTOS DE IDENTIDADES, IGUALDADES TRIGONOMÉTRICAS
Ecuaciones trigonométricas nivel 1
Ecuaciones trigonométricas nivel 2
Trigonometría ejercicios resueltos ( SI TIENES EXAMEN MIRA ESTO )
Te vas a transformar en una máquina de la trigonometría TUITEALO