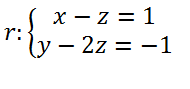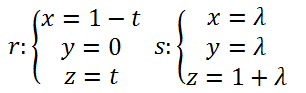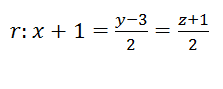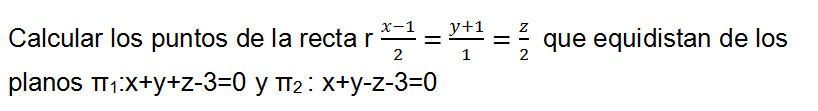👉 EJERCICIOS GEOMETRIA 2 BACHILLERATO resueltos de exámenes y selectividad . 🔥 Si pronto tienes examen de este tema , esta es tu página . Vamos a recapitular todos los problemas que hemos resueltos en vídeo para que puedas repasar , como siempre incidiremos en las claves del tema y os enseñaré algunos trucos para sacar la máxima nota posible en los exámenes .
Antes de empezar , si lo que necesitas es aprender el tema sigue este enlace ▶ TEMA TUTORIAL DESDE CERO DE GEOMETRÍA EN EL ESPACIO
Si lo que necesitas es hacer ejercicios para practicar para el examen , pues VAMOS A POR ELLOS MÁQUINA !! 🚂💪🚀
Ejercicios vectores en el espacio resueltos exámenes 2 bachillerato selectividad ebau evau
Ejercicio resuelto ver solución
Sean los puntos A( 1,0,2) B(0,1,1) y C( 1,1,0) calcula
a)Los vectores AB y AC
b) El producto escalar entre esos dos vectores , son perpendiculares
c) El ángulo entre los dos vectores
d) El producto vectorial entre los dos vectores
Ejercicio resuelto ver solución
Hallar a y b para que los vectores (a, −1,2) y (1,b, −2) sean perpendiculares y las dos primeras coordenadas de su producto vectorial sean iguales.
Ejercicio resuelto ver solución
Calcular un vector unitario perpendicular a los vectores (1,2,3) y ( 1,-2,-3 )
Ejercicio resuelto ver solución
Calcular un vector de módulo 4 que tenga la misma dirección, pero distinto sentido, que el vector ( 2,1,-2)
Ejercicio resuelto ver solución
¿Puede haber dos vectores de R3 tales que su producto escalar sea 3 y sus módulos 1 y 2 respectivamente ?
Ejercicio resuelto ver solución
Sean los puntos A(0,1,1) B(2,1,3) C(-1,2,0) Calcula el área del triángulo de vértices A, B y C
Ejercicio resuelto Ver solución
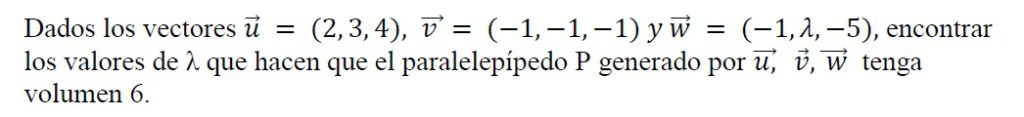
Si los videos te han servido , dale al LIKE y SUSCRIBETE 🚂 http://goo.gl/CMFnu0 y activa la campanilla🔥, en época de exámenes subimos muchos ejercicios clásicos de exámenes y así estarás informado ➡ compártelo por las redes sociales y grupos de clase 😉
Ejercicios resueltos ecuaciones de la recta y el plano
Ejercicio resuelto Ecuación del plano que pasa por tres puntos
Calcular la ecuación general del plano que pasa por A(-1,0,-1) B(-1,-1,0) C(0,1,-1)
Ejercicio resuelto recta perpendicular a un plano
Calcular la ecuación paramétrica de la recta que pasa por A(-1,0,3) y es perpendicular al plano π: x-y+3z=2
Ejercicio resuelto recta paralela a otra
Calcular la ecuación continúa de la recta que pasa por A(0,-2,1) y es paralela a
Ejercicio resuelto ecuación de un plano que contiene a dos rectas
Calcular la ecuación general del plano que contiene a las rectas que se cortan
Ejercicio resuelto ecuación de un plano que contiene dos rectas paralelas
MUY INTERESANTE
Calcular la ecuación general del plano que contiene a las rectas paralelas
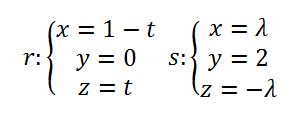
Aquí tienes el curso para ser una máquina de geometría en el espacio desde cero por si necesitas repasar algún apartado ▶ TEMA DE GEOMETRÍA EN EL ESPACIO
Si los videos te han servido , dale al 🔥 LIKE y SUSCRíBETE y activa la campanilla 🔔, en época de exámenes subimos muchos ejercicios clásicos de exámenes y así estarás informado ➡ compártelo por las redes sociales y grupos de clase 😉
Posiciones relativas Ejercicios resueltos
Posición relativa entre recta y plano
Estudiar la posición relativa entre la recta r y el plano π:x+y+z=2

Posición relativa entre rectas
Ejercicio resuelto
Estudiar la posición relativa entre las rectas

Posición relativa entre dos planos
Ejercicio 01
Estudiar la posición relativa entre los planos
a)π1:x-3y+2z=1; π2:-2x+6y-4z=3
b) π1:x-5y+3z=1; π2:-2x+2y-4z=1
c) π1:-2x+6y+4z=2 ; π2:x-3y-2z=-1
Posición relativa entre tres planos
Ejercicio
Estudiar la posición relativa entre los planos
π1:x-y+2z=1; π2:-2x-z=3 ; π3:2x+y=3
Ejercicio clásico de examen
Estudiar la posición relativa entre los planos y en caso de cortarse en una recta calcular su ecuación y un punto y el vector director de dicha recta.
π1:-x-y=1; π2:x+z=0 ; π3:y-z=-1
Ejercicios Posiciones relativas con parámetros resueltos
Ejercicio 01
Dados el plano π:2x +ay+4z=-25 y la recta r:

se pide,calcular los valores de a para los que la recta r está contenida en el plano
Ejercicio 02 clásico de examen rectas coplanarias
Dadas las rectas
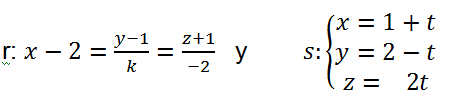
Hallar k para que las rectas sean coplanarias ver parte 1 ver parte 2
Selectividad CyL clásico de examen
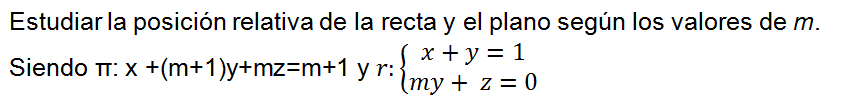
Ejercicios de distancias 2 bachillerato resueltos
Ejercicio resuelto
Calcular la distancia del punto P(1,0,-2) al plano π:-2x+3y+2z-1=0
Ejercicio resuelto
Calcular la distancia entre los planos π1:2x-y+z=3; π2:4x-2y+z=-1
Ejercicio resuelto
Calcular la distancia del plano π: x-y+2z-3 =0 a la recta r
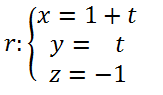
Ejercicios resueltos
Calcular la distancia del punto P(0,1,0) a la recta
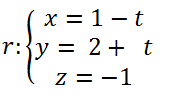
Ejercicios resueltos distancia rectas paralelas
Calcular las distancias entre las rectas r y s
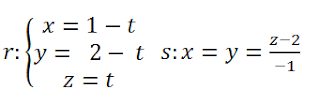
Ejercicios resueltos distancia rectas que se cruzan clásico de examen
Calcular las distancias entre las rectas r y s
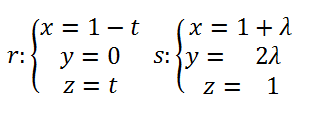
Si los videos te han servido , dale al 🔥 LIKE y SUSCRíBETE y activa la campanilla 🔔, en época de exámenes subimos muchos ejercicios clásicos de exámenes y así estarás informado ➡ compártelo por las redes sociales y grupos de clase 😉
Aquí tienes el curso para ser una máquina de geometría en el espacio desde cero por si necesitas repasar algún apartado ▶ TEMA DE GEOMETRÍA EN EL ESPACIO
Ángulos en el espacio R3
Ejercicio resuelto
Calcular el ángulo entre el plano π: x+3y+2z-3 =0 y la recta
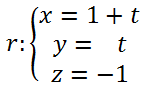
Ejercicio resuelto clásico de examen
Dados los puntos A(1,1,-2), B(3,-1,4) y la recta r : ( x=1+3λ; -2+5 λ; z=3 ) Se pide:
a) Calcular el área del triángulo OPQ, siendo O(0,0,0), P el punto medio del segmento AB y Q la intersección de la recta que pasa por A y B y el plano π:z=7
b) Hallar la ecuación del plano que pasa por A y es perpendicular a la recta r.
c) Calcular el coseno del ángulo que forman la recta r y la recta que pasa por A y B.
Ejercicios clásicos de examen
Los siguientes ejercicios son súper clásicos de examen , no hay casi exámenes de este tema en que no caiga al menos un problema de estos , así que vamos a meterle caña 💪💪💪
Simétrico de un punto respecto a una recta
Ejercicio resuelto
Determínese el punto simétrico de P(-3,1,-7) respecto a la recta
Simétrico de un punto respecto a un plano
Ejercicio resuelto
Determínese el punto simétrico de P(1,1,1) respecto al plano π: x-y+z=5
Recta simétrica a un plano
Dada la recta r≡x + 2 =y = z− 2 y el plano π ≡ x− z+ 2 = 0, se pide:
a) Determinar la posición relativa de r y π
b) Calcular el punto simétrico respecto de π del punto Pr(−2,0,2) y hallar la recta que es simétrica de r respecto del plano π.
Perpendicular común a dos rectas que se cruzan
Ejercicio resuelto ver solución
Calcular la perpendicular común a
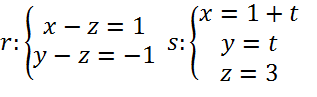
Recta que pasa por un punto y corta a otras dos Ejercico resuelto
Si los videos te han servido , dale al 🔥 LIKE y SUSCRíBETE y activa la campanilla 🔔, en época de exámenes subimos muchos ejercicios clásicos de exámenes y así estarás informado ➡ compártelo por las redes sociales y grupos de clase 😉
Aquí tienes el curso para ser una máquina de geometría en el espacio desde cero por si necesitas repasar algún apartado ▶ TEMA DE GEOMETRÍA EN EL ESPACIO
Ejercicios punto genérico de una recta resueltos
Quizás el apartado más complicado de este tema pero no te preoupes te enseñaré las claves y algunos Trucos para que domines este tipo de problemas ya que son bastante comunes en los exámenes
Como se que tienes muchísimas ganas de empezar 😉 vamos a por ello!!! 💪💪💪💪
Ejercicio Calcular los puntos de una recta que equidistan de dos planos Punto genérico
Ejercicio resuelto
Sean el plano π: x+y+z=0 y la recta r: x=y=z y el punto A(3,2,1) hallar el punto de r equidista de A y π
Algunos ejercicios de selectividad resueltos geometría 2 bachillerato
En los apartados anteriores hemos resuelto múltiples ejercicios de selectividad , insisto en que realices como mímimo todos los ejercicios clásicos de examen hasta ahora que por algo son clásicos .
Ahora vamos a resolver el resto de ejercicios de selectividad ebau evau..que tengo resueltos en vídeo y no he metido en los anteriores apartados
Ejercicio resuelto ver solución
Dados los puntos A(1,1,-2), B(3,-1,4) y la recta r : ( x=1+3λ; -2+5 λ; z=3 ) Se pide:
a) Calcular el área del triángulo OPQ, siendo O(0,0,0), P el punto medio del segmento AB y Q la intersección de la recta que pasa por A y B y el plano π:z=7
b) Hallar la ecuación del plano que pasa por A y es perpendicular a la recta r.
c) Calcular el coseno del ángulo que forman la recta r y la recta que pasa por A y B.
Ejercicio resuelto
Sean los puntos A(0,1,1), B(2,1,3), C(-1,2,0) y D(2,1,m).
(a) [0’75 puntos] Calcula m para que A, B, C y D estén en el mismo plano. Ver solución
(b) [0’75 puntos] Determina la ecuación del plano respecto del cual A y B son simétricos. Ver solución
(c) [1 punto] Calcula el área del triángulo de vértices A, B y C. Ver solución
Ejercicio
Se consideran los puntos P(2,3,1) y Q( 0,1,1)
Halla la ecuación del plano π respecto del cual P y Q son simétricos
Ejercicio
Si los videos te han servido , dale al 🔥 LIKE y SUSCRíBETE y activa la campanilla 🔔, en época de exámenes subimos muchos ejercicios clásicos de exámenes y así estarás informado ➡ compártelo por las redes sociales y grupos de clase 😉
CURSOS
Matemáticas 2º bachillerato ciencias y tecnológico
Matemáticas 2º bachillerato ciencias aplicadas a las ciencias sociales